怎样解释量子力学中的波函数（通俗易懂什么是量子态）

怎样解释量子力学中的波函数（通俗易懂什么是量子态）作用量（Action）——是一个物理系统内在的演化趋势；如一段运动的作用量，是动能与势能之差对时间的积分；其数值为，能量 * 时间（S = Et）或动量 * 位移（S = px），单位和普朗克常数一样（S = kh，k是倍数，h是普朗克常数）。普朗克常数——可以理解为“作用量”的单位，即：能量 * 时间 = 动量 * 位移 = 普朗克常数的倍数。在量子力学中：表征——是指用信息描述某一事物的状态，即：信息符号可以代替某一事物本身。量子态中的每种量子数，都是量子化的非连续数值，其取值只能是“某个最小量”的整数或是半奇数倍，这个最小量就是量子，其数值与普朗克常数有关，即以普朗克常数为单位，而一个量子化的系统，至少需要一个量子数。

迭代版本：161

本文，将会通俗易懂地介绍——量子态、波函数与粒子自旋的概念和图像，它们对于理解微观世界的奥妙（难以理解）与玄妙（难以想象），有着十分重要且基础的作用。

相信通过本文的描述，可以建立起对微观粒子世界，更清晰深刻的理解和认知。

主题目录如下：

• 什么是量子态
• 什么是波函数
• 量子态与波函数
• 什么是粒子自旋
• 自旋图像
• 自旋是如何发现的
• 不同自旋的含义
• 复合粒子的自旋
• 结语
• 后记：自旋与化学的微妙关系

什么是量子态

在量子力学中：

• 量子态——是由一组量子数所确定的微观状态。
• 量子数——是表征微观粒子运动状态的一些特定数值。
• 量子——是不可分割的最小量（如光量子即光子，是光的最小量）。
• 量子化——就是存在非连续，呈现离散数值的最小量（量子）。

表征——是指用信息描述某一事物的状态，即：信息符号可以代替某一事物本身。

量子态中的每种量子数，都是量子化的非连续数值，其取值只能是“某个最小量”的整数或是半奇数倍，这个最小量就是量子，其数值与普朗克常数有关，即以普朗克常数为单位，而一个量子化的系统，至少需要一个量子数。

普朗克常数——可以理解为“作用量”的单位，即：能量 * 时间 = 动量 * 位移 = 普朗克常数的倍数。

作用量（Action）——是一个物理系统内在的演化趋势；如一段运动的作用量，是动能与势能之差对时间的积分；其数值为，能量 * 时间（S = Et）或动量 * 位移（S = px），单位和普朗克常数一样（S = kh，k是倍数，h是普朗克常数）。

需要指出的是，光子碰巧是基本粒子，但并不是说量子就是基本粒子，只要是最小量即可——就如自旋角动量是最小量h / 2π的倍数，那么最小量h / 2π就是量子，这个量子的倍数就是自旋量子数，即量子数以量子为单位——不过，如果把基本粒子看成“小份能量”的同义词，那么视其为量子的近义词也未尝不可。

h / 2π——称为约化普朗克常数，h是普朗克常数，又写作“ℏ”，读作“h拔”。

量子数的数值，物理上代表着粒子可观测到的状态量，而在未观测之前，这些数值出现的可能性是叠加和纠缠的，其中：

叠加——是指量子数的数值是不确定的，每个数值出现的可能性，都是一个概率，于是不同数值出现的概率，就可以叠加在一起，其总和是100%。

例如，自旋量子数，可以上自旋出现的概率是50%，下自旋出现的概率是50%这样——上下自旋是Z轴上的方向，自旋在XY轴上也存在，即：X是左右自旋，Y是前后自旋——而上下自旋，就是量子数的两种数值，对应了两种量子态。

例如，薛猫的生死状态，如果由一个量子数来决定，那么量子数不同的数值，就代表了“生”的概率与“死”的概率，而在观测之前，薛猫就是处在了量子数“生死数值”的叠加态。

纠缠——是指一个量子数在不同的子系统上，其不同的数值仍然会相互协调，表现为一个数值在子系统上确定，那么与其叠加数值，在其它子系统上也会“瞬间”确定。

例如，一个自旋为0的粒子，衰变成了两个纠缠粒子，每个粒子都是上下自旋的叠加态，如果一个粒子被确定是上自旋（即随机到50%），那么另一个纠缠粒子不用测量（即不用在50%中随机）一定是下自旋——因为自旋会保持角动量守恒。

这就意味着，粒子的量子态是可以叠加和纠缠的，也就是通常所说的——量子叠加态与量子纠缠——前者就像是“上帝的骰子”，后者就像“上帝的意志”（即捉摸不定的运气）。

实际中，量子数有很多种，其中自旋量子数，也就是粒子自旋，而在描述原子核外电子运动状态时，有四种量子数：

• 主量子数（轨道能量层级，确定电子能级大小，正整数）。
• 角量子数（轨道空间角动量，确定电子云形状，正整数）。
• 磁量子数（轨道角动量的投影，确定电子云方向，整数）。
• 自旋量子数（自旋的方向，确定电子自旋方向，半奇数）。

例如，下图展示了氢原子的电子图像，包含了主量子数、角量子数、磁量子数——由于自旋量子数没有空间可见性，所以没有体现在图像中。

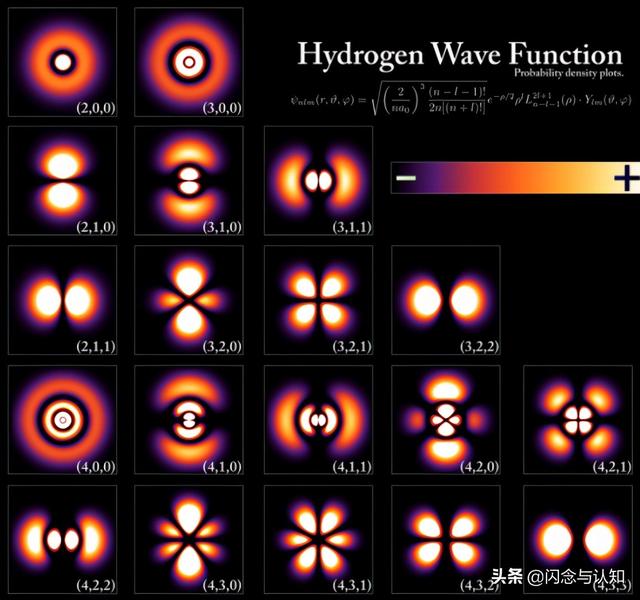
氢原子的电子云，右下角数字代表的是（主量子数，角量子数，磁量子数）对应（1能级，2形状，3方向），1代表不同的范围大小，1相同2代表不同的形状，2相同3代表不同的方向所看到的相同形状，图片来自维基百科（Wave function）

其它还有一些味量子数（Flavour），如重子数、轻子数、奇异数、同位旋等等，那么多个量子数就可以共同描述一个量子态，其中每个量子数在观测之前都是概率叠加，所以在观测之前，量子态就是多个量子数所有概率的叠加。

也就是说，用多个量子数每个可能的数值，进行排列组合（即数量相乘得到组合数，可见量子数必须是离散的），而每个组合都对应一个量子态的概率（即由组合中每个量子数的概率相乘得到），所有这些量子态的概率是叠加的，其总和是100%。

最后，量子态涉及到一个——泡利不相容原理（Pauli Exclusion Principle），即：自旋半奇数的粒子（即费米子），其组成的系统，不能有两个或两个以上的粒子，处在相同的量子态；而自旋整数的粒子（即玻色子），其组成的系统，则可以有多个粒子，处在同一个量子态。

也就是说，费米子系统——不能有全同粒子，量子态可计数；玻色子系统——可以有全同粒子，量子态不可计数。

量子态相同，就没有办法计数的原因在于，粒子没有明确的轨道，由于不确定性原理，它可以出现的位置是“概率云”，所以就没有办法追踪多个相同量子态中的一个，即不能给相同的量子态“编号”，这样多个相同的量子态就没办法区分，只能算一个，同时测量还会改变全同粒子的量子态，使其变得不同。

什么是波函数

在数学上，描述量子态的函数，就是——波函数，它是时间和空间的复变函数，其空间参数，是位置XYZ方向的三维组合，即ψ(x y z t)，其结果是复数（也看成是复向量空间的向量），而它的表达式，是在具体的微观条件下，由相应的薛定谔方程解出的。

复变函数（Complex Function）——是指以复数作为自变量和因变量的函数。

从某种角度说，薛定谔方程描述了粒子（包括原子及亚原子），其能量与动能、势能的关系，即：总能量 = 动能 势能——方程可以描述一对多的关系，函数只能描述一对一的关系——而薛定谔方程解出的波函数，则描述了粒子，其状态与时间、空间的映射关系，这个映射关系在薛定谔方程中，就决定了粒子能量随时间的演化，即：

总能量 * 波函数 = 动能 * 波函数 势能 * 波函数。

需要指出的是，如果粒子的总能量是一个定值，即总能量不随时间演化，这样的粒子状态就被称为“定态”，那么描述定态的薛定谔方程就不含时间，所以就被称为“定态薛定谔方程”。

例如，原子内部的电子，就具有确定的能量状态（即定态），它可以被定态薛定谔方程描述。

薛定谔方程——iℏ * (∂t)ψ(r t) = (-ℏ^2 / 2m) * (∂r^2)ψ(r t) V(r t) * ψ(r t)，i是虚数，ℏ约化普朗克常数，r是XYZ坐标，t是时间，∂t是波函数在t方向上的偏导，∂r^2是波函数在XYZ三个方向上的二阶偏导再求和，m是粒子质量，V是粒子势能。

方程等式的左边是总能量，右边是动能和势能，即：总能量（波函数关于时间的变化，∂t）= 动能（波函数关于空间的变化，∂r^2） 势能（波函数所在场的变化，V）——可见方程中，没有一阶以上的变量（线性）且有未知函数（波函数）及其二阶偏导（微分），所以它是一个线性二阶偏微分方程。

定态薛定谔方程——Eψ(r) = (-ℏ^2 / 2m) * (∂r^2)ψ(r) V(r) * ψ(r)，E是粒子的总能量是一个定值，定态方程不含时间，也就是假设势能V(r)和波函数ψ(r)都与时间无关，即不随时间变化，这种不含时波函数称为定态波函数，但其仍具有波动性，代表了粒子自身与时间无关的空间波动性。

事实上，量子力学中的薛定谔方程，就像是经典力学中的牛顿方程，它的表达式来自牛顿方程的“粒子化”，整个方程建立在各种假设之上，其正确性由实验保证，并且它只适用于低速的非相对论粒子（狭义相对论），也不包含自旋描述——当涉及到相对论效应与自旋时，由狄拉克方程描述（其中也有波函数），可见狄拉克方程就像经典力学中的狭相方程。

有趣的是，“波函数”起初只是一个数学函数，虽然物理学家薛定谔，通过假设“凑出”了薛定谔方程，但他并没有“理解”波函数，而是物理学家玻恩，对波函数做出了正确的“概率诠释”，或说“统计诠释”。

需要指出的是，物理学诠释只是对“真理”的一种解释，而解释可以有很多种，所以物理学诠释并不唯一，但得到共识且符合实验观测的诠释，就可以获得诺贝尔奖，如玻恩对波函数的概率诠释。

相比解释（Explain），诠释（Annotation）不仅说明原因关联，还具有某种代表性的独特理解。

那么，之所以称之为波函数，是因为薛定谔方程在数学上，是一种类型的波动方程，而波函数又产生并解释了粒子的波粒二象性，所以描述量子态的函数，其实是在描述一种“波”。

在物理上，波函数的图像，即ψ(x)，就代表了粒子位置的概率分布（类似正弦波的形状），其模平方，即|ψ(x)|^2，就是粒子位置的概率密度，而通过概率密度可以得出，粒子在某位置的概率。

需要指出的是，波函数的物理意义——是量子力学（哥本哈根学派）的一个基本假设，不需要推导，也不需要解释，只需要默认接受即可。

换言之，波函数是粒子的概率分布函数，取值为复数，物理意义为概率幅度（Probability Amplitude）；波函数的模平方是粒子的概率密度函数，取值为正实数，物理意义为区域概率。

纵轴是波函数的实部，蓝线是概率幅度，红线是区域概率，红色透明度代表了粒子在x位置出现的概率，图片来自维基百科（Wave function）

概率分布函数——取值是小于某值的概率，如：P = F(b)，这个概率是小于某值（b）的概率累加，那么它可以计算某个区间的概率，如：P = F(b) - F(a)，而区间斜率越大，说明概率的变化率越大，即F(b) - F(a)越大，也就是概率越大，这个变化率（或说导数）就是概率密度。

概率密度函数——取值是概率的变化率，那么它在某个区间的面积越大，就是随机到其中的概率越大，也就是概率密度的面积（或说积分）是某个区间的概率分布，而这个变化率越大，如f(a)越大，表明在该点（a）附近的概率越大，但不是该点（a）的概率越大，不过这个变化率可以理解为，在该点（a）无穷小区域内的概率。

复数的模——就是系数平方和的平方根，如：|a bi| = |a - bi| = sqrt(a^2 b^2)。

从物理角度绘景，波函数就像是一个“复数场”，场里的每一个复数都是波的幅度，其模平方是波的概率，其方向（即复向量的向量角）是波的相位。

相位（Phase）——就是一个波，其循环中的位置，如：波峰、波谷、或是峰谷之间某个点的标度。

需要注意的是，波函数的干涉叠加，是概率幅度的叠加，而不是概率（即模平方）的叠加，两者是有区别的，即：“先相加再模平方”与“先模平方再相加”的区别；如：|0.1 0.1|^2 = 0.04与|0.1|^2 |0.1|^2 = 0.02的结果是不一样的。

综上可见，波函数就是粒子所具有的概率波动性，因此波函数也被称为——概率波，或波粒二象性中的物质波。

量子态与波函数

具体来说，量子态与波函数有着微妙的关系，即：

量子态在数学上称之为“态向量”（State Vector，或称“状态向量”），它是复向量空间上的一个复向量——关键在于，态向量（即量子态）在被波函数描述之前，是“不可见”的，这就像一个向量必须被投影到坐标系上，才能描述出来被“看见”——可见波函数，其实是量子态（即态向量）在坐标系上的投影。

需要指出的是，物理上的矢量就是数学上的向量，矢量存在于真实空间，向量存在于数学空间，所以态向量在物理上被称为“态矢量”，而由于态矢量（数学抽象）必须由波函数（坐标表象）描述，所以波函数也被称为“态函数”，态矢量则可以简称为“态”。

换言之，量子态这个向量，在某些基底（即基向量）方向上的投影，就是波函数，所以波函数也是一个向量（可以用一维矩阵表示这个波函数向量），只不过这个向量具有概率波动性——其模平方就是，粒子在此向量处出现的概率，而这个向量可以看成是，波函数“波形图像”的相位。

那么显然，一个向量可以由多个基底方向上的向量来线性叠加组合，所以一个量子态就可以由多个波函数线性叠加组合来描述，而每个波函数都是一个量子态的投影，这意味着一个量子态可以由多个量子态线性叠加表示，即：量子叠加态（它是薛定谔方程的一个解）。

需要注意的是，波函数ψ(x)所有的取值，都是其向量的分量，每一个分量也是向量——分量代表了波函数“波形图像”上某处的幅度和相位——如果有无穷多个分量（如位置坐标），叠加态就要使用积分代替求和。

可见，波函数蕴含了所有可能的状态，每一个状态都是一个向量，而所有这些向量之和，则就是“波函数向量”。

例如，量子态ψ，由量子态ψ1和ψ2叠加，即：|ψ> = a|ψ1> b|ψ2>，符号“| >”中的ψ、ψ1、ψ2只是一个名称用于标识量子态、量子数或物理操作等，而每一个“| >”都是一个基底量子态，前面的系数a、b的值是复数，也就是波函数对应的取值，所以系数就是波函数，代表了这个量子态出现的概率。

量子态的符号——量子态ψ，用右矢“|ψ>”或左矢“<ψ|”表示，由于其数值是一个复数，所以右矢和左矢就是共轭复数，即实部相同且虚部不同的复数，而从向量角度看，右矢|ψ>是一维列向量，左矢<ψ|是一维行向量。

需要指出的是，基底量子态又称为“本征态”（Eigen State），通俗地说，就是可以被观测到的量子态，从这个角度看，量子叠加态就是——任意多个可以被观测到的本征态的系数线性叠加（也就是波函数的线性叠加），并且所有系数对应的概率相加必须得到100%，即：实际中必须要能（也只能）观测到，任意多个本征态中的某一个。

需要注意的是，波函数虽然是复数，但其投影的本征态的复数轴可能为0（即与复数轴垂直），此时这个本征态对应的系数（即波函数、复数、向量）就没有虚数i。

例如，|薛猫生死态> = a|生的本征态> b|死的本征态>，其中a（波函数、复数、向量）决定了生的概率，b（波函数、复数、向量）则决定了死的概率——如果生或死的概率都是50%，那么a = 1 / sqrt(2)，b = i / sqrt(2)，|a|^2 |b|^2 = 1，这里假设要求本征态的概率之和是100%——如果是两个波函数的干涉叠加，则其概率是|a b|^2，而不是|a|^2 |b|^2。

本征（Eigen）——就是事物本身的特征。

在数学上，可用公式表达，即：pf = cf，p是操作，f是映射，c是常数，意思是一个映射的操作结果等于这个映射的常数倍，可见这个操作的效果就是常数倍的缩放，所以常数（c）就是操作（p）的本征值（Eigen Value）。

在物理上，操作p就是一种物理变换（也称算符），映射f（数学上称算子）可以是函数（态函数）或向量（态矢量），所以可以称之为本征态（Eigen State）或本征向量（Eigen Vector），可见本征态和本征向量经过算符的操作，只是缩放其状态和方向不变。

事实上，波函数也可以用量子态的符号表示，那么上述量子态叠加就可以写成：|ψ> = |a> <a | ψ> |b> <b | ψ>，其中<a | ψ>就是量子态ψ在本征态a方向上的投影，<a | ψ>就是波函数ψ(a)，其模平方就是量子态ψ在本征态a方向上出现的概率。

所以，波函数有两种表示形式：

• 从ψ(x)函数形式看——是将x映射到一个复数；
• 从<x | ψ>量子态形式看——是将量子态ψ投影到本征态x。

而向量的投影，其实就是向量的内积，因此<x | ψ>就是量子态ψ与本征态x的内积——可见波函数ψ(x)，就是向量内积的产物。

那么，如果x不是本征态，而是另一个量子态ψ2 ，此时<ψ2 | ψ1>就表示波函数ψ1和波函数ψ2的内积，意思是量子态ψ1坍缩到量子态ψ2的概率（这是玻恩规则，量子力学的一个基本假设），其结果仍然是一个波函数、复数、向量——自然也是量子态ψ1到量子态ψ2的投影。

但一个波函数与其自身（共轭复数）的内积，就表示其模平方，即：<ψ | ψ> = |ψ|^2，意思是（前面所说的）量子态ψ的概率密度，其结果是一个正实数——可以理解为，自身的投影就从“复数世界”投影到“实数世界”去了。

而如果一个波函数，是叠加态（或称混态）则<ψ | ψ> = 1（这是量子力学的一个基本假设，即这个向量的空间内积被归一化），是非叠加态（或称纯态）则<ψ | ψ>小于1，表示叠加态（如薛猫生死态）在某个本征态（如薛猫生的态）上的投影概率。

回到量子数的角度，一个粒子的量子态，可以由多个量子数描述，所以波函数其实是描述了多个量子数叠加的概率分布，如：ψ(r p E s t)，r是位置，p是动量，E是能量，s是自旋——这相当于，将连续（如位置）和离散（自旋）的变量都放到了一个多维向量中来描述。

换言之，波函数可以给出特定“位置、动量、能量、自旋”状态粒子的概率分布——其概率依然是波函数的模平方，即：|ψ(r p E s t)|^2——事实上，所有的量子数都与“位置、动量、能量、自旋”有对应关系，因此波函数就可以描述所有的量子数。

需要指出的是，在数学上，函数的一个参数就是一个维度，而超过四维参数（即三维位置和一维时间）的超空间，都可以投影到四维的位置空间或动量空间。

因为，时间与能量有对应关系（时间平移对称性的守恒量是能量），空间与动量有对应关系（空间平移对称性的守恒量是动量）——别忘了，物理系统的演化，可以用“作用量”描述，而作用量 = 能量 * 时间 = 动量 * 位移 = 普朗克常数的倍数——所以波函数可以写成，随时间与能量变化的位置函数（对应位置空间）与动量函数（对应动量空间）。

那么，观测一个粒子的量子态，就相当于获取了粒子的量子数，于是波函数对应的概率密度，就会坍缩到一个确定的点上，即概率随机出结果（观测到本征态），这也就是——“波函数坍缩”，而此时，波函数就演化成了一个“确定态”的函数（不再具有“叠加态”），于是粒子的波动性也就变成了粒子性。

最后，总结一下，量子态是一个数学抽象，需要用波函数具体描述（表示），那么：

• 在数学上，波函数映射了，复数（函数值）与时间、空间（函数参数），其图像是一个波形，而将复数看成复向量空间的一个复向量，则波函数代表了所有映射向量的叠加向量，即态向量（也是一个复向量）。
• 在物理上，波函数映射了，粒子状态的概率幅度（函数值）与时间、空间（函数参数），其图像是一个概率分布，而将概率幅度的模平方看成是概率，则波函数包含了所有状态概率的叠加概率，即量子态（也是一个态矢量）。

可见，数学描述了量子态（叠加向量），物理则诠释了量子态（叠加概率）。

什么是粒子自旋

粒子自旋——是粒子的重要属性，可以用来对粒子的标识和分类，因为每个粒子都有特有的自旋，自旋数不同就是不同类别的粒子，性质也不同。

但粒子自旋，并不对应宏观上的物体自转，如：陀螺自转、地球自转——因为点粒子没有转轴以外的部分（其它点），也没有更小单元围绕质心自转。

所以，粒子自旋是唯象（Phenomenology）的描述，仅能将自旋视为一种内在性质，是粒子与生俱来带有的一种角动量。

角动量——是质点矢径扫过面积的速度大小，或是刚体定轴转动的剧烈程度 。

而自旋具有可观测的量子化数值——无法被改变，但其方向可以透过一些操作来改变，并且自旋（角动量）与方向（角度）遵循不确定性原理，即：自旋可以分解到XYZ坐标轴方向，每个方向的自旋就会此消彼长——也就是说，确定一个Z方向的上下自旋，就不能确定另外XY方向的自旋。

弦理论专家——布赖恩·格林（Brian Greene），在《宇宙的琴弦》中，指出：

“宇宙的每一个电子，总是永远地以固定不变的速率旋转。电子自旋不是我们习惯的那类物体偶然发生的短暂的旋转运动，而是一种内禀的性质，跟它的质量和电荷一样。如果电子没有自旋，它也就不是电子了。”

自旋图像

一个自旋纠缠的光子，“翅膀”就是叠加态的自旋，图片来自影片《宇宙时空之旅：未知世界》

最后“翅膀”合并了，是量子自旋纠缠态坍缩了，图片来自《宇宙时空之旅：未知世界》

自旋是如何发现的

首先，是在斯特恩-盖拉赫实验中（Stern-Gerlach Experiment），发现了银原子束经过不均匀磁场，产生了偏转，并最终在屏幕垂直方向上，形成了两个上下对称的非连续分布。

预期是一条线，实际是两个点，图片来自维基百科（Stern-Gerlach Experiment）

这里有两个奇怪的事情：

第一，为什么银原子电中性，会被磁场影响？

这是因为，银原子有一个非配对电子，这个电子绕着原子核的轨道运动，形成了闭环电流，而闭环电流会产生磁矩，正是这个磁矩，让银原子产生了偏转。

磁矩——就是磁场中的磁性力矩，方向垂直于线圈所在平面，且当电流方向为逆时针时磁矩为正，顺时针时为负。

需要注意的是，如果是均匀磁场，闭环电流的磁矩就是0，只有不均匀的磁场，才能产生垂直方向上的磁矩。

第二，为什么屏幕上，预期是连续分布，但实验结果却是非连续分布？

这是因为理论上，银原子电子的磁矩方向，是随机连续的，其取决于电子的轨道角动量——也就是说，电子云与垂直方向有一个随机连续的角度。

那么，拥有不同磁矩方向的银原子，进入不均匀磁场，就会有不同的固定偏转，而大量不同磁矩方向的银原子，最终在屏幕垂直方向上，就应该是随机连续分布的。

而实验结果表明，电子的轨道角动量不是连续的，而是量子化的，也就是电子云与垂直方向的角度只有两个固定值，所以银原子的磁矩就只有上下两个固定值。

但如果是这样，就会存在一个问题，就是根据理论：

• 轨道角量子数，只能是正整数，即：l = 0，1，2，等等中的一个。
• 轨道磁量子数，受制角量子数，即：针对每一个角量子数l，磁量子数都可以取值为——从 l到-l之间的整数，如：l = 1对应1，0，-1；l = 2对应2，1，0，-1，-2——也就是有2l 1个可能的数值，代表着磁矩可能的方向。

那么在实验中，银原子的磁矩有上下两个，即：2l 1 = 2得出l = 1 / 2，然而电子角量子数——并不能等于非正整数。

要解决这个问题，就可以假设电子自身，拥有一个半奇数（1 / 2）的自旋量子数，然后自旋角动量磁矩与轨道角动量磁矩，其“合磁矩”才是银原子（基态）的两个磁矩。

这等同于说，银原子角动量 = 电子轨道角动量 电子自旋角动量——于是，电子自旋就被引出了。

其次，在实验之后，物理学家狄拉克，用狄拉克方程解出了“自旋解”——它是狄拉克方程内在的数学要求。

至此，所有的粒子从理论上就都有了——自旋。

不同自旋的含义

粒子的自旋角动量，是可观测的量子化数值，其值是——自旋量子 * 自旋量子数 ，其中自旋量子是h / 2π，而自旋量子数是整数或半奇数，可正负代表了不同的自旋方向。

• 自旋为0——粒子，从各个方向看都一样，就像一个点（如希格斯玻色子）。
• 自旋为1——粒子，在旋转360度（1圈）后看起来一样（如光子、胶子）。
• 自旋为2——粒子，在旋转180度（1 / 2圈）后看起来一样（如引力子，未证实）。
• 自旋为1 / 2——粒子，在旋转720度（2圈）后才会看起来一样（如电子、中微子、夸克）。
• 目前发现的粒子中——自旋为整数的，最大自旋为4，自旋为半奇数的，最大自旋为3 / 2。

A中黑桃的方向360度还原，K中人物的方向180度还原，图片来自《物理史话》

事实上，自旋为s的粒子通常有2s 1种自旋，如：自旋1 / 2的电子有2种自旋，自旋1的光子有3种自旋，自旋为0的希子（希格子玻色子）有1种自旋。

那么，对于自旋1 / 2，反映到波函数（即概率波的图像）上——就是粒子转一圈之后，波函数的相位会与原来的正好相反，只有转2圈，波函数才能彻底恢复原状。

当然，直接测量波函数的相位，是不可能的，但是我们可以测量相位差。 就像双峰干涉实验一样，相位差不同的两束波，叠加在一起会发生干涉现象。这样的话，通过干涉条纹的分布，就可以计算出相位差，也就可以证明粒子自旋，确实是1 / 2了。

不过，在现实中，物理学家费曼曾用水杯演示了，需要旋转2圈（即720度）才能复原的情况，如下图所示：

费曼的水杯自旋表演，360度到540度，需要手过头顶才能完成，图片来自科学网《统一路-7-奇妙的旋转2》

那么，对应到泡利不相容原理，在费米子系统中，粒子的量子态之所以不能相同，就在于费米子自旋整数圈不能对称，只有自旋半整数圈才对称。

这意味着，费米子波函数不具有交换对称性，只有交换反对称性，即：交换费米子位置，其波函数就会改变正负号。

因此，费米子波函数的对称中心点，就必须是0（否则就没有反对称性），而这个点，就是量子态相同的点，其出现费米子的概率是0，即：没有量子态相同的费米子。

对此，英国粒子物理学家——布莱恩·考克斯（Brian Cox），在《量子宇宙》中，指出：

“可以证明，自旋就是不相容原理的原因，因此也是原子结构之所以如此的原因……现在我们知道了，我们鞋的原子包含的电子与地面的电子，不仅是由于同性电荷相斥而相互推开；根据泡利不相容原理，它们也因自然的互相避开而排斥。”

可见，正是自旋带来的相互排斥力（即简并压力，Degeneracy Pressure），才使得原子具有结构稳定性，从而支撑了原子之上的结构稳定性——显然，这也是我们体内原子具有结构稳定性的原因所在。

复合粒子的自旋

复合粒子，是由基本粒子构成的，基本粒子是不可再分的点粒子。这里不可分割的意思，是指没有体积与模型图像，无法检测到其内部结构，如：光子、电子和夸克。

那么，复合粒子的自旋——就是其内部各组成部分之间，相对轨道角动量和各组成部分自旋的向量和，即：按照量子力学中，角动量相加法则求和，如质子的自旋——可以从夸克和胶子的自旋得到。

结语

综上可见，量子态通过多个量子数，描述了微观粒子的运动状态，量子数代表的，就是微观粒子，最小的不可分割的一个状态性质，可以称之为——“自由度”。

而自由度，可以理解为状态呈现的一些数值——这些数值是量子化的，即不连续、跳动、随机的，显然这是非常“自由”的，所以波函数也是自由度的函数。

在众多量子数中，自旋是所有微观粒子，所普遍共有的，那为什么所有的粒子都要自旋呢？

这和波函数坍缩一样，目前是一个未解之谜。

后记：自旋与化学的微妙关系

我们知道，化学元素即是原子，而元素的化学性质，是由原子其核外电子的数量与排列，所决定的——于是，元素的化学性质，就和电子绕核运动所具有的能量，关联在了一起。

由前文可知，电子绕核运动的状态，由四个量子数来描述，即：主量子数（n），角量子数（l），磁量子数（m），自旋（s）——而它们之间约束关系，就决定了核外电子的数量与排列，即元素的化学性质。

具体来说：

• n是电子的能级，取正整数，如：n = 0，1，2，3，等等。
• l是电子的形状，取正整数，且每个n对应[0 n-1]个l，如：n = 1对应l = 0；n = 2对应l = 0，1；n = 3对应l = 0，1，2；即：l = n。
• m是电子的方向，取整数，且每个l对应[-l l]个m，如：l = 0对应m = 0；l = 1对应m = -1，0，1；l = 2对应m = -2，-1，0，1，2；即：m = 2l 1
• s是电子的自旋，取半奇数，固定对应两个数值，即：- 1 / 2与 1 / 2。

那么，代入物理意义就是，电子在特定的能级（n）只能有数量有限的形状（l = n），在特定的形状（l）只能有数量有限的方向（m = 2l 1），在特定的方向（m）只能有两个自旋数值——所以，m个方向就有2m个不同的电子。

于是，电子数量就被能级给固定了，即：电子数量 = 2m = 2(2l 1)，且l = [0 n-1]，如：

• 能级n = 1则l = 0——可以容纳2个电子。
• 能级n = 2则l = 0，1——可以容纳2 6 = 8个电子。
• 能级n = 3则l = 0，1，2——可以容纳2 6 10 = 18个电子。

类氢原子轨道，从上到下：能级大小n = 1，2，3；轨道形状l = 1（s轨道），2（s-p轨道），3（s-p-d轨道）；轨道投影方向m = 1s，1s 3p = 4，1s 3p 5d = 9；自旋没有空间可见性，图片来自维基百科（Quantum number）

至于，为什么一个能级在一个形状和方向上，最多只能放2个电子——这是前文所提到的，泡利不相容原理的要求，即：电子的量子态不能相同，而电子自旋只有两个数值，来区分相同形状和方向上的量子态。

更为底层的一个原理是，万物总是趋向于处在最低能量状态——对原子来说，就是总是倾向于用电子填充其能级（否则就会增加其自身的能量），于是原子就会有动力与相邻的原子共用电子，而这就是化学作用的基础。

例如，氢原子外层n = 1能级有1个电子，但可以填充2个电子，于是它与另一个氢原子共用1个电子，就形成了氢分子H2。

例如，碳原子有两个能级，外层n = 2能级有4个电子（内层n = 1有2个电子，一共6个电子），但可以填充8个电子，于是再结合4个氢原子的电子，就形成了甲烷CH4。

例如，氧原子有两个能级，外层n = 2能级有6个电子（内层n = 1有2个电子，一共8个电子），于是再结合2个氢原子的电子，就形成了水H2O，而它也可以一对结合一个碳原子的4个电子，从而形成二氧化碳CO2。

可见，正是自旋决定了原子核外电子的排列方式，才形成了元素之间相互结合的驱动力，最终才形成了从氢、氧、碳、到水与基因，等大自然中的万物。