k means聚类算法的原理及步骤(机器学习经典算法之k-means聚类)
k means聚类算法的原理及步骤(机器学习经典算法之k-means聚类)print(__doc__) # Author: Phil Roth <mr.phil.roth@gmail.com> # License: BSD 3 clause import numpy as np import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn.datasets import make_blobs plt.figure(figsize=(12 12)) n_samples = 1500 random_state = 170 X y = make_blobs(n_samples=n_samples random_state=random_state) # Incorrect number of clusters y_pred = K
聚类就是将某个数据集中的样本按照之间的某些区别划分为若干个不相交的子集,我们把每个子集称为一个“簇”。划分完成后,每个簇都可能对应着某一个类别;需说明的是,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构,簇对应的概念语义由使用者来把握和命名。
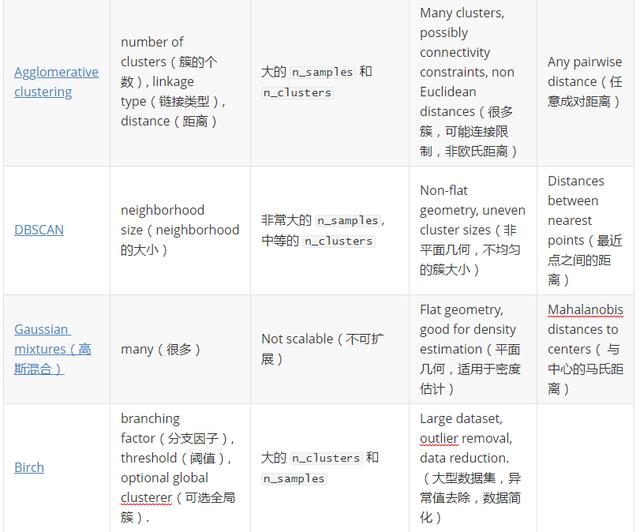
有关聚类的算法很多,下面这张表格引用自Scikit-learn 官方文档,从这张表中可以看到各个聚类算法之间的不同以及对不同数据及划分时的匹配程度,和优劣性。我们在选择聚类算法的时候,首先一定要熟悉自己的数据,大概了解自己的数据是怎样的一个分布和结构。这样,有利于我们选择合适的算法,从而得到优秀的聚类结果。这篇文章仅仅介绍K-means聚类算法,以及它的推广版K-mean 算法。


k-means算法是使用最广泛的聚类算法之一。聚类的目的是把相似的样本聚到一起,把不相似的样本分开。对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
K-means算法旨在选择一个质心 能够最小化惯性或簇内平方和的标准:
$$\sum{i=0}^{n} \min _{\mu{j} \in C}\left(\left|x{i}-\mu{j}\right|^{2}\right)$$
K-means算法原理分析
k-means算法是聚类分析中使用最广泛的算法之一。它把n个对象根据它们的属性分为k个簇以便使得所获得的簇满足:同一簇中的对象相似度较高;而不同簇中的对象相似度较小。 k-means算法的基本过程如下所示:
- 首先随机选取K个初始质心,最基本的方法是从数据集$X$中选择$K$个样本。
- 将每个样本分配到其最近的质心。通过取分配给前一个质心的所有样本的平均值来创建新的质心。
- 计算新旧质心之间的差值,算法重复最后两个步骤,直到该值小于阈值。换句话说,算法重复这个步骤,直到质心不再明显移动。
下图是Scikit-learn具体实现代码:
print(__doc__)
# Author: Phil Roth <mr.phil.roth@gmail.com>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
plt.figure(figsize=(12 12))
n_samples = 1500
random_state = 170
X y = make_blobs(n_samples=n_samples random_state=random_state)
# Incorrect number of clusters
y_pred = KMeans(n_clusters=2 random_state=random_state).fit_predict(X)
plt.subplot(221)
plt.scatter(X[: 0] X[: 1] c=y_pred)
plt.title("Incorrect Number of Blobs")
# Anisotropicly distributed data
transformation = [[0.60834549 -0.63667341] [-0.40887718 0.85253229]]
X_aniso = np.dot(X transformation)
y_pred = KMeans(n_clusters=3 random_state=random_state).fit_predict(X_aniso)
plt.subplot(222)
plt.scatter(X_aniso[: 0] X_aniso[: 1] c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
# Different variance
X_varied y_varied = make_blobs(n_samples=n_samples
cluster_std=[1.0 2.5 0.5]
random_state=random_state)
y_pred = KMeans(n_clusters=3 random_state=random_state).fit_predict(X_varied)
plt.subplot(223)
plt.scatter(X_varied[: 0] X_varied[: 1] c=y_pred)
plt.title("Unequal Variance")
# Unevenly sized blobs
X_filtered = np.vstack((X[y == 0][:500] X[y == 1][:100] X[y == 2][:10]))
y_pred = KMeans(n_clusters=3
random_state=random_state).fit_predict(X_filtered)
plt.subplot(224)
plt.scatter(X_filtered[: 0] X_filtered[: 1] c=y_pred)
plt.title("Unevenly Sized Blobs")
plt.show()
K-means算法的优缺点
优点:简单,易于理解和实现;收敛快,一般仅需5-10次迭代即可,高效
缺点:
- 对K值得选取把握不同对结果有很大的不同(初始化不同质心的计算通常会进行几次。帮助解决这个问题的一种方法是 k-means 初始化方案,它已经在 scikit-learn 中实现(使用 init='k-means ' 参数)。 这将初始化质心(通常)彼此远离,相对随机初始化得到更好的结果)
- 对于初始点的选取敏感,不同的随机初始点得到的聚类结果可能完全不同
- 对于不是凸的数据集比较难收敛
- 对噪点过于敏感,因为算法是根据基于均值的
- 结果不一定是全局最优,只能保证局部最优
- 对球形簇的分组效果较好,对非球型簇、不同尺寸、不同密度的簇分组效果不好。
K-means算法的优缺点
优点:简单,易于理解和实现;收敛快,一般仅需5-10次迭代即可,高效
缺点:
- 对K值得选取把握不同对结果有很大的不同(初始化不同质心的计算通常会进行几次。帮助解决这个问题的一种方法是 k-means 初始化方案,它已经在 scikit-learn 中实现(使用 init='k-means ' 参数)。 这将初始化质心(通常)彼此远离,相对随机初始化得到更好的结果)
- 对于初始点的选取敏感,不同的随机初始点得到的聚类结果可能完全不同
- 对于不是凸的数据集比较难收敛
- 对噪点过于敏感,因为算法是根据基于均值的
- 结果不一定是全局最优,只能保证局部最优
- 对球形簇的分组效果较好,对非球型簇、不同尺寸、不同密度的簇分组效果不好。
(1)获取更多优质内容及精彩资讯,可前往:https://www.cda.cn/?seo
(2)了解更多数据领域的优质课程:





