指数一次型函数（4.2指数函数）

指数一次型函数（4.2指数函数）指数不同底数不同，通过中间量来比较。指数相同底数不同，利用幂函数的单调性来判断。例:2.如何比较指数幂大小 。指数不同底数相同，利用指数函数的单调性来判断。

指数函数的性质:

1.如何解决与指数函数有关的复合函数的单调性问题。

(1)形如y=af(x)(a>0 且a≠1)的函数的单调性的判断方法:当a>1时 函数u=f(x)的单调递增(减)区间即为函数y=af(x)的单调递增(减)区间;当0<a<1时 函数u=f(x)的单调减(增)区间即为函数y=af(x)的单调递增(减)区间.

2.形如y=f(aⅹ)(a>0 且a≠1)的函数的单调性的判断方法:通过内层函数u=aⅹ的取值范围确定外层函数y= f(u)的定义域 在此定义域内讨论外层函数的单调区间，再根据复合函数“同增异减”的规律确定复合函数的单调区间。

例:

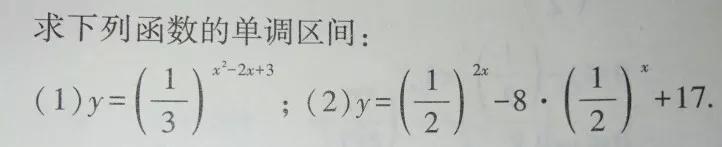
2.如何比较指数幂大小 。

指数不同底数相同，利用指数函数的单调性来判断。

指数相同底数不同，利用幂函数的单调性来判断。

指数不同底数不同，通过中间量来比较。

例: