正多边形与对应的圆有什么关系?正多边形外接圆与内切圆形成的圆环
正多边形与对应的圆有什么关系?正多边形外接圆与内切圆形成的圆环如图,设边长为1的正方形,求正方形的外接圆与内切圆形成圆环的面积。接着,我们来了解一下正方形的外接圆与内切圆所形成圆环的面积。 ∴BD=CD=1/2 ∴OD=√3/6 ,OC=√3/3 S圆环=S外接-S内切=(√3/3)2π-(√3/6)2π=1/4π
初中数学,圆环是有两个同心的圆所构成,那么关于圆环的面积,相信大家都知道该如何求解,那么关于正多边形的外接圆与内切圆所形成的圆环,它的面积是多少呢,有什么规律呢。今天为就大家讲讲。

首先,我们来分析一下正三角形的外接圆与内切圆所形成圆环的面积。
如图,设边长为1的正△ABC,求△ABC的外接圆与内切圆形成圆环的面积。
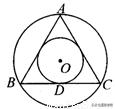
解析:连接OC,作OD⊥BC于D
∴BD=CD=1/2
∴OD=√3/6 ,OC=√3/3
S圆环=S外接-S内切=(√3/3)2π-(√3/6)2π=1/4π
接着,我们来了解一下正方形的外接圆与内切圆所形成圆环的面积。
如图,设边长为1的正方形,求正方形的外接圆与内切圆形成圆环的面积。

解析:连接OA,作OD⊥AB于D
∴AD=BD=1/2
∴OD=1/2 ,OC=√2/2
S圆环=S外接-S内切=(√2/2)2π-(1/2 )2π=1/4π
接着,我们来了解一下正六边形的外接圆与内切圆所形成圆环的面积。

如图,设边长为1的正六边形,求正六边形的外接圆与内切圆形成圆环的面积。

解析:连接OA,作OD⊥AB于D
∴AD=BD=1/2
∴OD=√3/2 ,OC=1
S圆环=S外接-S内切=(1)2π-(√3/2 )2π=1/4π

通过上面例题的分析,我们可以知道,正三角形,正四边形,正六边形它们的外接圆与内切圆所形成的圆环,圆环的面积都为正多边形边长的1/4π倍。掌握这个规律,可以帮我们快速解答类似的题目,让我们节约更多的学习时间。那今天就为大家分享到这里,希望这些东西对大家有用。祝大家学习愉快。




