中考数学圆的压轴题切割线定理（怎么求关于圆的动点）

中考数学圆的压轴题切割线定理（怎么求关于圆的动点）根据切线的判定和结论：∠BCD=∠ADC=90°，CD为圆O的直径，则AD、BC为圆O的切线；根据正方形的性质和题目中的条件：四边形ABCD为正方形，则AB=BC=CD=AD，∠A=∠B=∠BCD=∠ADC=90°；（2）当△EOF是等腰三角形时，求t的值。1、当EF与半圆相切时，求t的值设EF与半圆的切点为G，连接OG，过点E作EM⊥BC于点M

点击右上角关注“陈老师初中数理化”分享学习经验，一起畅游快乐的学习生活。

关于圆的动点问题是数学中考的重要题型，本文就例题详细解析这类题型的解题思路，希望能给初三学生的数学学习带来帮助。

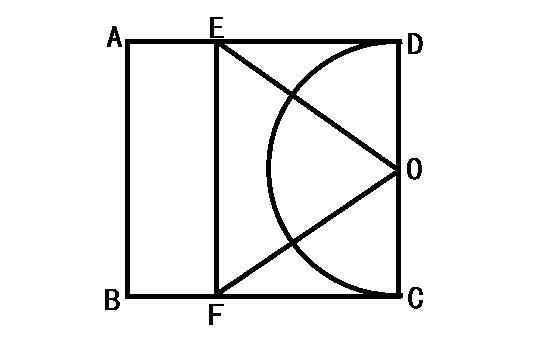
例题

在正方形ABCD中，有一直径为CD的半圆，圆心为O，CD=2，现有两点E，F，分别从点A，C同时出发，点E沿线段AD以每秒1个单位长度的速度向点D运动，点F沿线段CB以每秒2个单位长度的速度向点B运动，当点F运动到点B时，点E也随之停止运动，设点E离开点A的时间为t（s）。

（1）当EF与半圆相切时，求t的值；

（2）当△EOF是等腰三角形时，求t的值。

1、当EF与半圆相切时，求t的值

设EF与半圆的切点为G，连接OG，过点E作EM⊥BC于点M

根据正方形的性质和题目中的条件：四边形ABCD为正方形，则AB=BC=CD=AD，∠A=∠B=∠BCD=∠ADC=90°；

根据切线的判定和结论：∠BCD=∠ADC=90°，CD为圆O的直径，则AD、BC为圆O的切线；

根据切线长定理和结论：EF、AD、BC为圆O的切线，则EG=ED，FG=CF；

根据结论：EG=ED，FG=CF，则EF=EG FG=ED CF；

根据题目中的条件：点E以每秒1个单位长度的速度运动，点F以每秒2个单位长度的速度运动，运动时间t，则点E的运动距离AE=t，点F的运动距离CF=2t；

根据结论：AE=t，CD=AD=2，则ED=AD-AE=2-t；

根据结论：EF=ED CF，ED=2-t，CF=2t，则EF=2 t；

根据题目中条件：EM⊥BC，则∠BME=90°；

根据矩形的判定和结论：∠A=∠B=∠BME=90°，则四边形ABME为矩形；

根据矩形的性质和结论：四边形ABME为矩形，AB=2，AE=t，则EM=AB=2，AE=BM=t；

根据结论：BM=t，BC=2，CF=2t，则MF=BC-BM-CF=2-3t；

根据勾股定理和结论：EM⊥BC，EM=2，MF=2-3t，EF=2 t，EF^2=EM^2 MF^2，则t=1 √2/2或1-√2/2；

当t=1 √2/2时，CF=2t=2 √2>BC，不符合条件，舍去；

所以，当EF与半圆相切时，t=1-√2/2。

2、当△EOF是等腰三角形时，求t的值

（1）EO=FO

根据全等三角形的判定和题目中的条件：CO=DO，∠BCD=∠ADC=90°，EO=FO，则△EDO≌△FCO；

根据全等三角形的性质和结论：△EDO≌△FCO，则ED=CF；

根据结论：ED=2-t，CF=2t，ED=CF，则t=2/3；

（2）EF=FO

过点F作FN⊥AD于点N

根据题目中的条件：FN⊥AD，则∠ANF=90°；

根据矩形的判定和结论：∠A=∠B=∠ANF=90°，则四边形ABFN为矩形；

根据矩形的性质和结论：四边形ABFN为矩形，则AN=BF，AB=FN=2；

根据题目中的条件和结论：CF=2t，BC=2，则BF=2-2t；

根据结论：AN=BF，BF=2-2t，则AN=2-2t；

根据结论：AE=t，AN=2-2t，则NE=AE-AN=t-2 2t=3t-2；

根据勾股定理和结论：∠ANF=90°，NE=3t-2，FN=2，EF^2=NE^2 FN^2，则EF^2=9t^2-12t 8；

根据勾股定理和结论：∠BCD=90°，CF=2t，CO=CD/2=1，OF^2=CF^2 CO^2，则OF^2=4t^2 1；

根据结论：EF^2=9t^2-12t 8，OF^2=4t^2 1，EF=OF，则t=1或5；

当t=5时，CF=2t=10>BC，不符合条件，舍去；

（3）EF=OE

根据勾股定理和结论：∠ADC=90°，DE=AD-AE=2-t，DO=CD/2=1，OE^2=DE^2 DO^2，则OE=t^2-4t 5；

根据结论：OE=t^2-4t 5，EF^2=9t^2-12t 8，EF=OE，则t无解；

所以，当△EOF是等腰三角形时，t=2/3或1。

结语

解决本题的关键根据动点的运动规律，用含t的代数式表示出线段长度；利用圆的切线和全等三角形性质，得到线段之间的等量关系；再根据勾股定理列方程求解，就可以得到题目需要的值。