任意三角形面积相等的条件:三角形面积相等的条件如何利用
任意三角形面积相等的条件:三角形面积相等的条件如何利用问题在关键在于,怎么找到D'点呢?回到我们寻找等面积三角形的过程上来,从三角形名称上,△ABC和△ABD的公共边是AB,于是这条边便可作公共底,在直线CD上,任意一点到AB的距离都相等,因为平行线间距离相等,即无论直线CD上哪一点作为三角形顶点,面积总是和△ABC相等。刚才在计算的过程中,其实已经找到了一个点D,但是千万不要忘记,直线AB另一侧,即点B上方还有一个点也满足要求,如下图:很简单对吧?相信不少学生会求出点B坐标,然后用割补法来求,这当然没错,同时,要明白除了割补法之外,还有其它方法,例如过点C作AB的平行线CD,它与y轴交点为D点,而此时的△ABD与△ABC面积相等,直线CD斜率与直线AB相同,而点C坐标已知,因此解析式好求,为y=-3/4x 9/4,于是点D坐标为(0 9/4),面积更容易得到,为7.5;第二个例子将上题增加一个小问,在y轴上找一点D,使△ABD与△ABC面积
从面积相等的三角形说起

关于几何图形面积的计算,是从小学便开始学习了,今天我们聊的话题是三角形的面积,当然,计算公式都知道,底与高乘积的一半。而在中考压轴题中,再次遇到它,便不仅仅直接用它计算这么简单,通常情况下,我们会面临两个三角形面积相等的情况。从面积计算公式角度来看,无非是这两个三角形底与高的乘积相等,而又细分为等高或等底两种情况;从几何图形关系来看,无非是全等或割补。
第一个例子
如图,平面直角坐标系中,直线y=-3/4x 6与y轴交于点B,点A(4 3)在直线上,点C(4 0)在x轴上,求△ABC的面积。

很简单对吧?相信不少学生会求出点B坐标,然后用割补法来求,这当然没错,同时,要明白除了割补法之外,还有其它方法,例如过点C作AB的平行线CD,它与y轴交点为D点,而此时的△ABD与△ABC面积相等,直线CD斜率与直线AB相同,而点C坐标已知,因此解析式好求,为y=-3/4x 9/4,于是点D坐标为(0 9/4),面积更容易得到,为7.5;

第二个例子
将上题增加一个小问,在y轴上找一点D,使△ABD与△ABC面积相等。
刚才在计算的过程中,其实已经找到了一个点D,但是千万不要忘记,直线AB另一侧,即点B上方还有一个点也满足要求,如下图:

问题在关键在于,怎么找到D'点呢?回到我们寻找等面积三角形的过程上来,从三角形名称上,△ABC和△ABD的公共边是AB,于是这条边便可作公共底,在直线CD上,任意一点到AB的距离都相等,因为平行线间距离相等,即无论直线CD上哪一点作为三角形顶点,面积总是和△ABC相等。
这个原理同样适用于另外一根平行线,关键在于距离!平行线间的距离。
在上图中,我们将这个距离作出来,如下图:

图中,△BGD和△BHD'全等是极容易证明的结论,因此,当BG=BH时,BD=BD',因此我们寻找另外一根直线时,并不需要将距离画出来,而是直接在y轴上截取BD'=BD,因为我们知道,虽然截取的线段并不是距离,但它们相等却能保证距离相等。
第三个例子
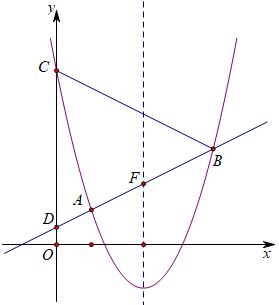
如图,在平面直角坐标系中,以直线y=5/2为对称轴的抛物线y=ax² bx c与直线l:y=kx m(k>0)交于A(1 1),与y轴交于C(0 5),直线与y轴交于点D。
(1)求抛物线的函数表达式;
(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若AF:FB=3:4,且△BCG与△BCD面积相等,求点G的坐标;
(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值。
解析:
(1)从阅读题目条件中,我们可首先确定解析式中的字母c=5,然后由对称轴可得-b/2a=5/2,于是b=-5a,最后把点A坐标代入y=ax²-5ax 5,求得a=1,于是y=x²-5x 5;
(2)抛物线一旦确定,那么随之点B坐标可确定,毕竟它与点A的关联紧密,AF:FB=3:4,极易联想到相似三角形,而构造相似三角形的最佳方式则是向x轴作垂线,AM,BN,如下图:

注意观察图中三条平行线AM∥FH∥BN,由平行线分线段成比例,可知MH:HN=AF:FB=3:4,而其中线段MH=3/2,于是HN=2,顺利求得点B(9/2 11/4),于是直线AB解析式为y=1/2x 1/2,则D(0 1/2),现在可以用前面归纳的方法来寻找点G了,BC为公共底,于是我们在y轴上找到点D关于点C的对称点D',然后分别过D和D'作BC的平行线,如下图:

显然我们找到了对称轴右侧的两个点,直线BC解析式为y=-1/2x 5,而直线DG与直线D'G'的解析式分别为y=-1/2x 1/2和y=-1/2x 19/2,它们与抛物线的交点即为所求,分别为G(3 -1)和G'((9 3√17)/4 (67-3√17)/4)。
(3)在x轴上找一点P使∠APB=90°,不妨将△ABP找出来观察,按条件描述,它是一个直角三角形,直角顶点在x轴上,非常自然地想到构造“一线三直角”模型,并且在前一问中,已经过点A,B面x轴作了垂线了,只要不擦,连暗示都省了,如下图:

图中△AMP∽△PNB,只需要将对应边用含字母的代数式表示即可,先消参,将点A坐标代入直线y=kx m中,得到m=1-k,于是y=kx 1-k,与抛物线解析式联立得kx 1-k=x²-5x 5,整理并解出两根,其中之一为点B横坐标,于是B(k 4 k² 3k 1),此时便有办法列比例式得到关于k的方程了,但为了进一步减轻计算量,不妨多思考一下,以AB为直径的圆,点P在圆周上,题目条件中说有且仅有一点,则意味着该圆与x轴相切,如下图:

显然可证P为MN中点,得点P(1/2k 5/2 0),再来列比例式,则容易多了,整理后得3k² 6k-5=0,同时注意k>0,解得k=-1 2√6/3。
解题反思:
三角形面积相等的运用,由浅入深,本质其实一样,利用平行线来寻找无疑较便捷,但这种思想是需要平时进行渗透的,一味只懂得割补法,或者停留在割补法的成功,不愿意再研究新的方法,遇到这道题,思路通顺的可能性就低,或者被解析法中复杂的高次方程吓退。
平时的课堂教学中,老师需要根据学生实情,选择不同的解题方法进行重点讲解,不同层次的学生会有不同收获。解题中同样存在形式主义,即只要能解出来,方法无所谓。其实方法用哪一种确实无所谓,但尝试的解法种类多,相当于为学生打开了新视野,一个视野开阔的学生,思维同样开阔,当遇到困难的时候,不会一条路走到黑,而是会及时调整思路,从而更容易找到正确的那条。
一个班级40多名学生,对某种解题方法的理解各不相同,而一节课时间又有限,这些解法并不能保证在课堂上全部讲透,那么,摸清学生思维习惯,从而在课堂上讲多数学生习惯理解的方法,然后课余再进行拓展,鼓励学生一题多解,这件事要坚持做,虽然对批改作业和个别辅导要求更高,但学生收获最大。
爱数学做数学




